Modeling
Machine learning models are becoming increasingly popular for data and simulation-driven design and analysis of systems. The only basic requirements for machine learning (ML) modeling are the existence of an underlying pattern to be learned, the availability of data characterizing the patterns, and justification for ML models versus mathematical models (computational cost, inability to represent the pattern mathematically). Typical use-cases include training surrogate models of computationally expensive simulators, creating purely data-driven models where no analytical or other models exist, time series prediction and forecasting, training accurate models by combining varying fidelities and sources of data, surrogate models for use in optimization, etc.
Selected Research
Sparse Gaussian Processes / Large-Scale Learning
As problem dimensionality increases, the size of the training set must also grow proportionally in order to capture varying patterns across the several dimensions. Artificial neural networks (ANN) have proven to be effective for large-scale high-dimensional problems and there has been interest in developing Bayesian modeling techniques (that provide uncertainty estimates of prediction as well) that can scale and perform well in high-dimensions as well. The ‘vanilla’ Gaussian process (GP) formulation incurs a complexity of O(n^3) in inference, where n is the size of the training set. This is due to the Cholesky decomposition operation involved during a matrix inversion operation as part of inference. Improvements have been made in the form of sparse Gaussian processes and structured Gaussian processes that exploit structure in training data (e.g., data along rectilinear grids) in order to leverage Kronecker algebra to accelerate inference [1]. This allows GP inference for datasets in the order of millions of points [2,3].
[1] Flaxman, S., Wilson, A., Neill, D., Nickisch, H., & Smola, A. (2015, June). Fast Kronecker inference in Gaussian processes with non-Gaussian likelihoods. In International Conference on Machine Learning (pp. 607-616).
[2] Singh, P., Couckuyt, I., Elsayed, K., Deschrijver, D., & Dhaene, T. (2017). Multi-objective geometry optimization of a gas cyclone using triple-fidelity co-kriging surrogate models. Journal of Optimization Theory and Applications, 175(1), 172-193.
[3] Singh, P., & Hellander, A. (2017, December). Surrogate assisted model reduction for stochastic biochemical reaction networks. In Proceedings of the 2017 Winter Simulation Conference (p. 138). IEEE Press.
Deep Learning
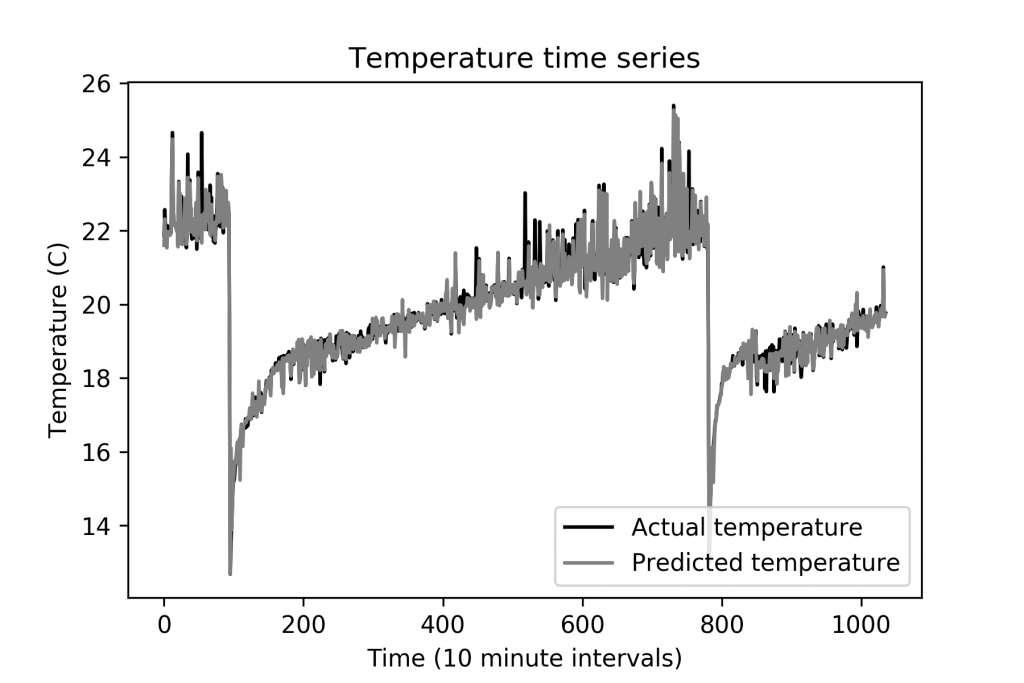
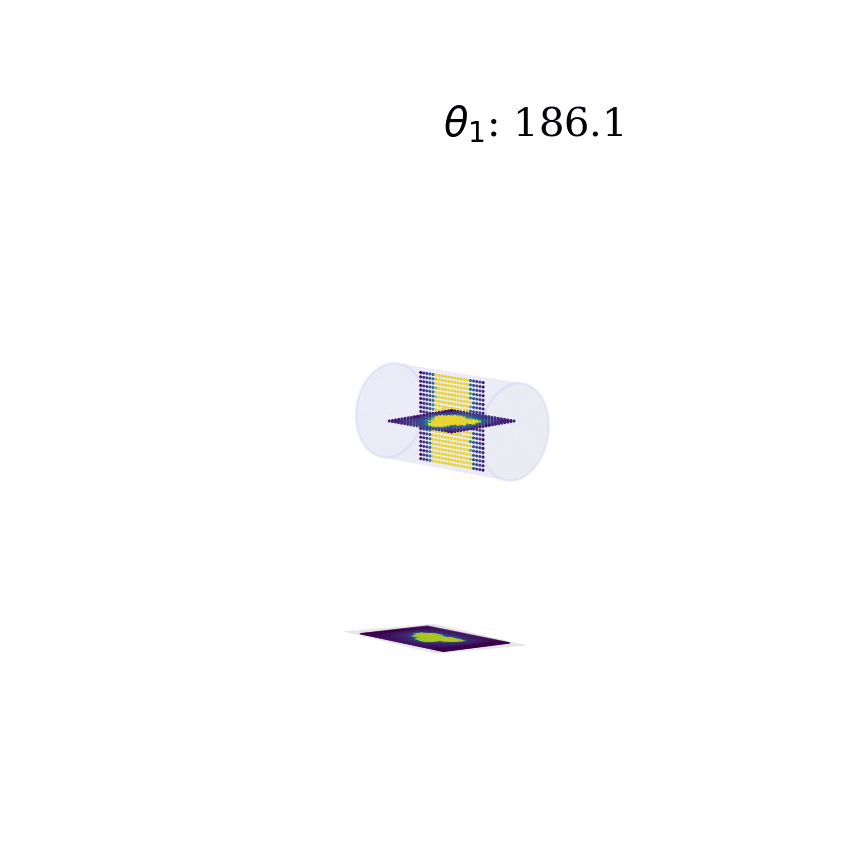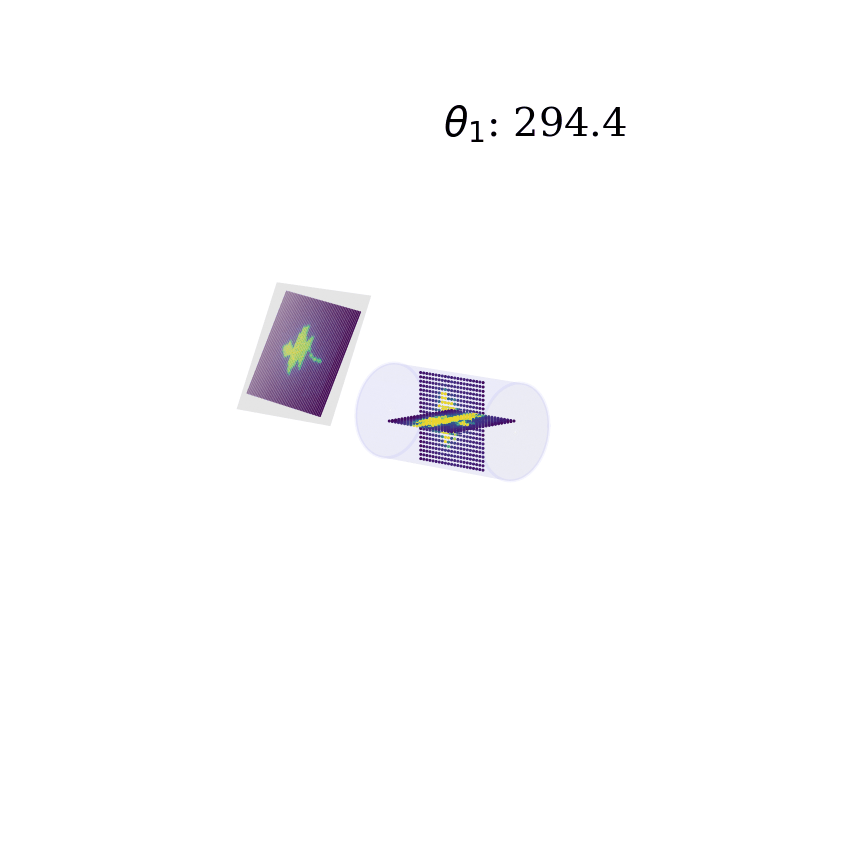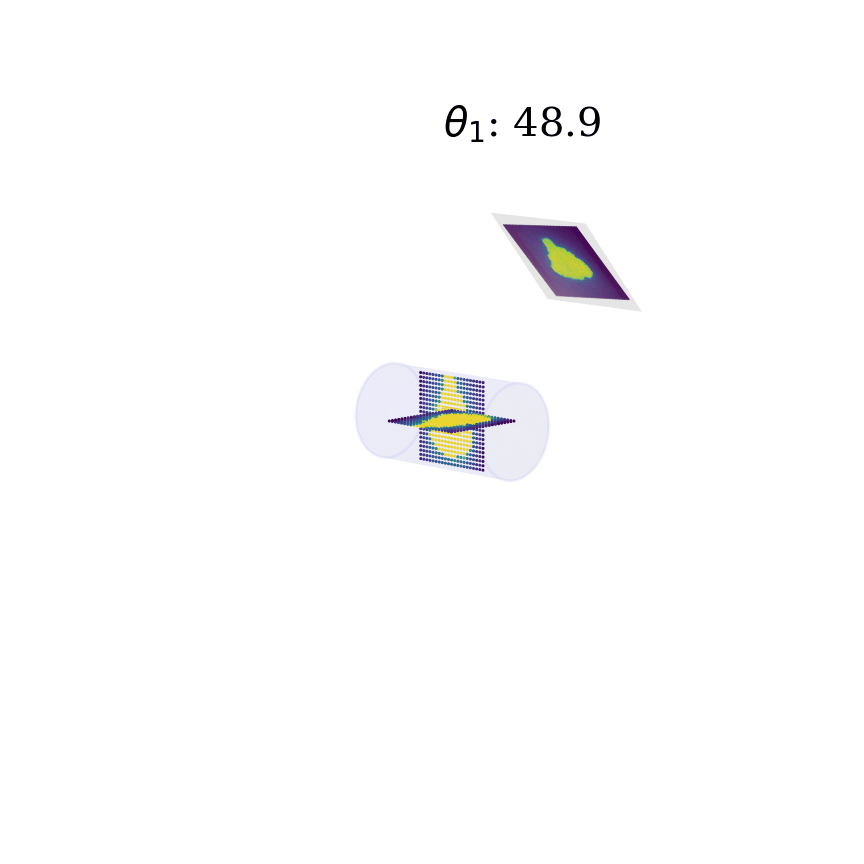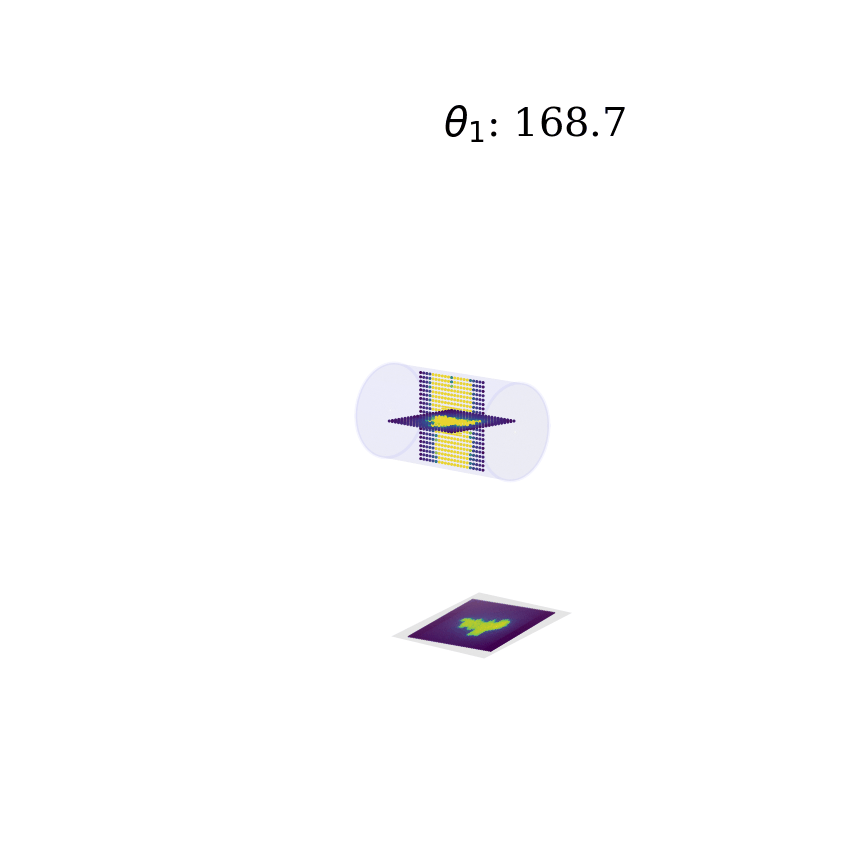
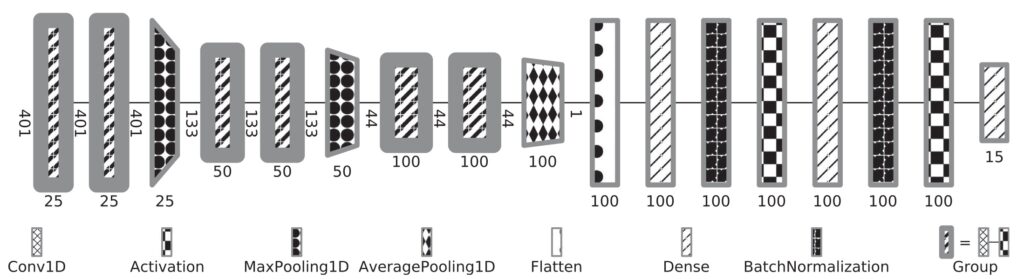
Deep neural networks have gained mass popularity in recent times for applications involving moderate-to-large datasets. Their ability to learn highly non-linear patterns makes them applicable to even challenging high-dimensional problems. For example, the highly non-linear time series of temperature variation of machines in a data centre has been modeled using LSTM neural networks in [1]. The figure on the right-top shows the learned patterns of one such machine.
Another example is presented in master thesis project [2] where a combination of neural networks is used to learn the phantom dose distribution patterns for dosage calibration as part of radiation therapy (figure right-bottom). Although the angular and spatial variations make learning the patterns challenging, novel de-noising and angular adjustment techniques using regression neural networks deliver highly accurate pattern characterization.
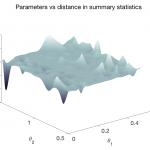
Our most recent work in deep learning concerns learning expressive summary statistics of high-dimensional stochastic time series responses, for likelihood-free parameter inference [3,4].
[1] Singh, P., Elamin, M., & Toor, S. (2020, June). Towards Smart e-Infrastructures – A Community Driven Approach Based on Real Datasets. In Proceedings of the 2020 IEEE GreenTech Conference. IEEE Press.
[2] Åkesson, M. (2019). Learning Phantom Dose Distribution using Regression Artificial Neural Networks (Dissertation). Retrieved from http://urn.kb.se/resolve?urn=urn:nbn:se:uu:diva-380767
[3] Åkesson, M., Singh, P., Wrede, F., & Hellander, A. (2021). Convolutional neural networks as summary statistics for approximate bayesian computation. IEEE/ACM Transactions on Computational Biology and Bioinformatics.
[4] Wrede, F., Eriksson, R., Jiang, R., Petzold, L., Engblom, S., Hellander, A., & Singh, P. (2022, July). Robust and integrative Bayesian neural networks for likelihood-free parameter inference. In 2022 International Joint Conference on Neural Networks (IJCNN) (pp. 1-10). IEEE.
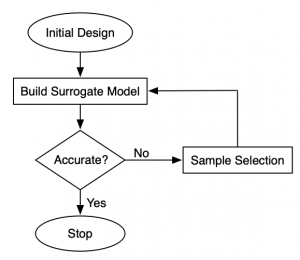
Surrogate Modeling
Surrogate models (also known as metamodels and response surface models) are popular as replacements of computationally expensive functions such as CFD models, responses of microwave filters, antennae etc, and as data-driven models of phenomena that is hard to represent mathematically. In cases where it is possible to select training data freely (e.g., data from simulations), a sequential sampling algorithm can be used to prepare the training set. The figure on the right depicts a typical surrogate modeling flowchart. One begins with a small set of (usually) space-filling samples known as the initial design, and then samples are iteratively added in small batches. In each iteration, the surrogate model is re-trained and tested for accuracy. One can stop as soon as required accuracy thresholds are met, thereby minimizing the number of data samples needed to train an accurate model.
Sequential sampling for global surrogate modeling is an established research area in its own right. A deeper There exist sequential sampling algorithms for both regression [1] and classification [2] surrogate models. discussion on the sampling aspects can be found here.
[1] Singh, P., Deschrijver, D., & Dhaene, T. (2013, December). A balanced sequential design strategy for global surrogate modeling. In 2013 Winter Simulations Conference (WSC) (pp. 2172-2179). IEEE.
[2] Singh, P., Van Der Herten, J., Deschrijver, D., Couckuyt, I., & Dhaene, T. (2017). A sequential sampling strategy for adaptive classification of computationally expensive data. Structural and Multidisciplinary Optimization, 55(4), 1425-1438.
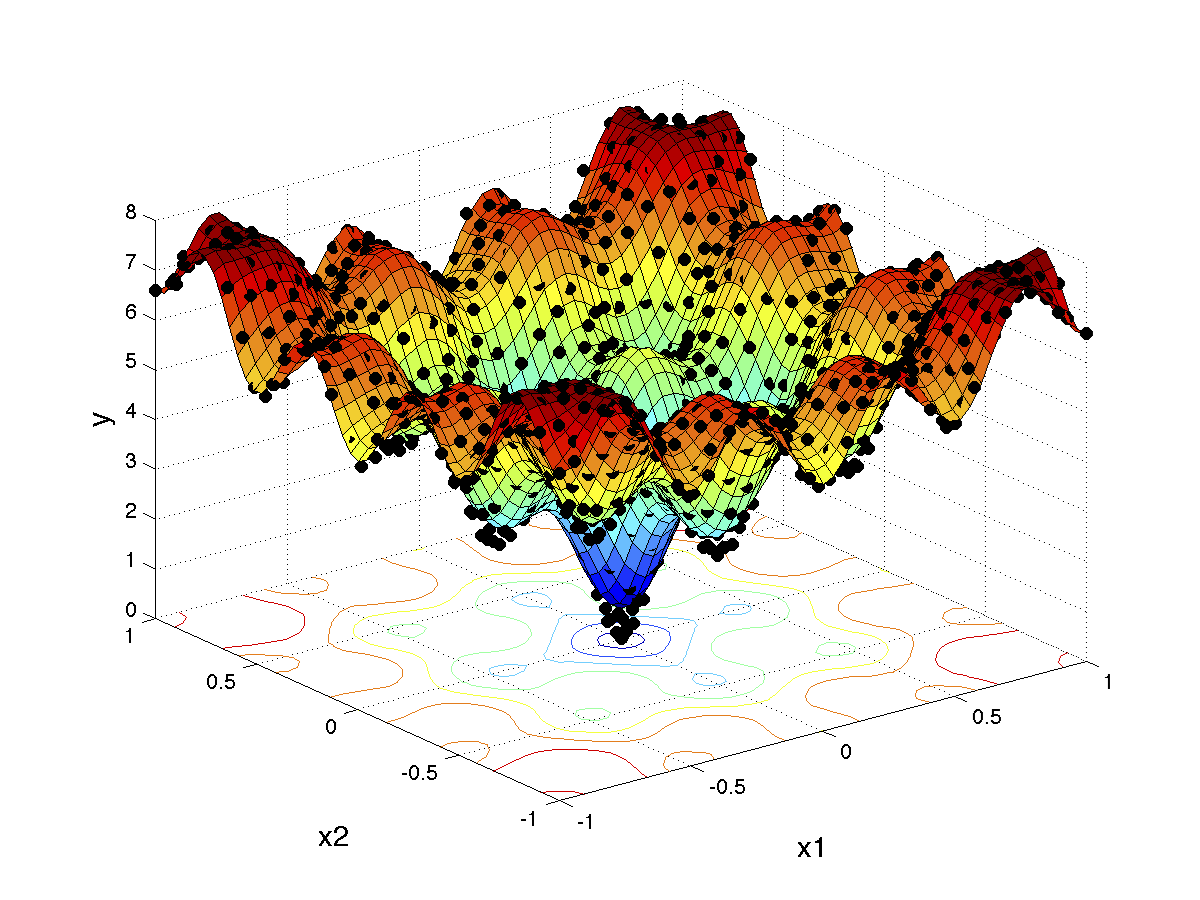
Co-Kriging / Multi-Fidelity Modeling with Gaussian Processes
A recursive co-Kriging model [1] formulation assumes the presence of a scaling factor to combine two separately trained Kriging models (Kriging and Gaussian processes are very closely related). In general, there will be (k-1) scaling factors for k data fidelities. Given multiple fidelities of data, a Kriging model can be trained per fidelity and the scaling factors can be estimated during training.
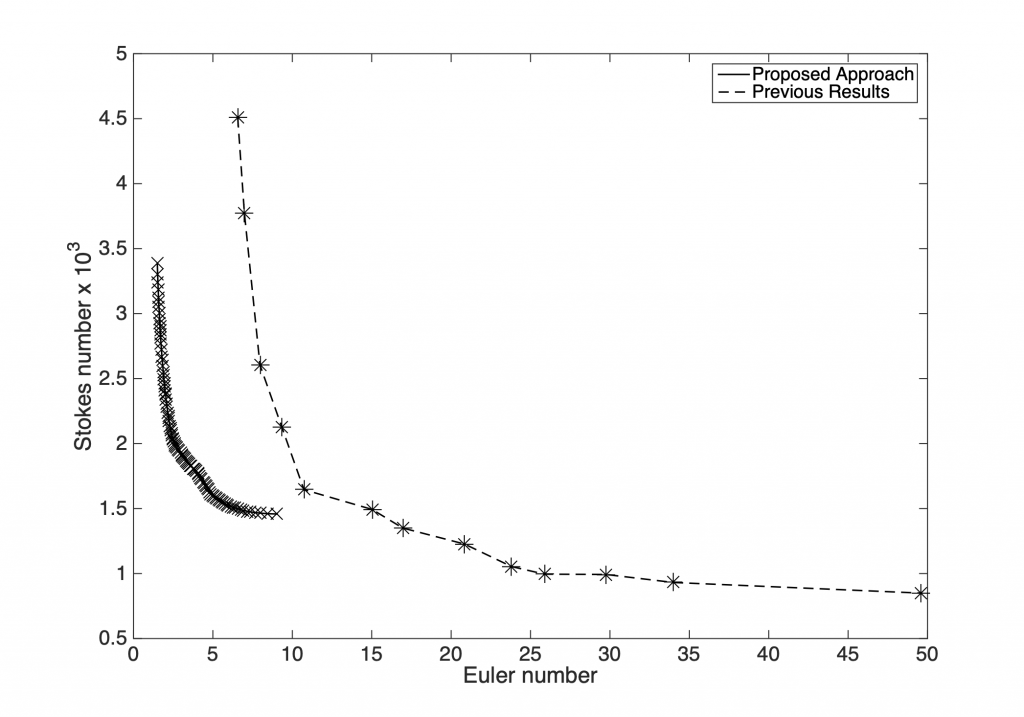
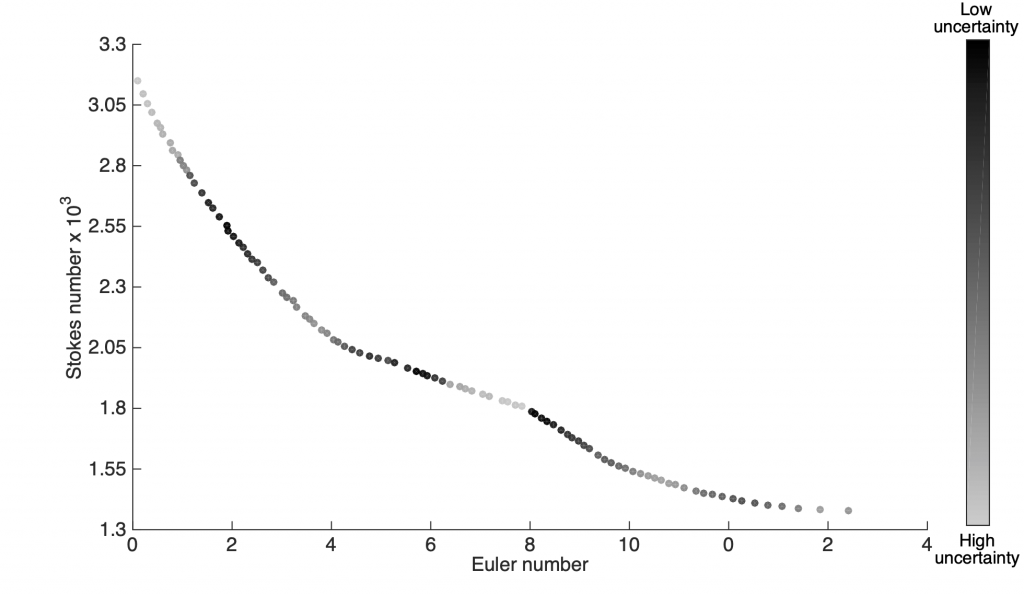
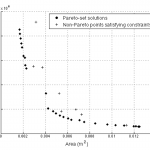
The ability to incorporate information from different fidelities allows the co-Kriging model to be more accurate than a single fidelity model. The images on the right correspond to a triple-fidelity co-Kriging model trained to model a cyclone separator from very limited experimental data (highest fidelity), limited amount of CFD simulation data (medium fidelity) and voluminous data from analytical models (cheap/low fidelity). Evolutionary optimization using the co-Kriging model as a surrogate yields a very fine Pareto front (closer to the origin of the first plot) significantly improving over results from Bayesian optimization using analytical models as data source. Another advantage of co-Kriging (and in general, Bayesian models) is the ability to get uncertainty estimates in addition to the predictions themselves. The figure on the right, bottom shows uncertainty estimates from the co-Kriging model.
[1] Singh, P., Couckuyt, I., Elsayed, K., Deschrijver, D., & Dhaene, T. (2017). Multi-objective geometry optimization of a gas cyclone using triple-fidelity co-kriging surrogate models. Journal of Optimization Theory and Applications, 175(1), 172-193.