Parameter Inference
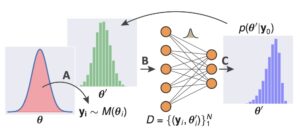
The parameter inference problem involves inferring the parameters of a descriptive model (e.g., simulator) from observed data. In cases where the likelihood function corresponding to the model is available, techniques such as maximum likelihood estimation (MLE) can be used. A more interesting case is of likelihood-free parameter inference where inference must proceed solely based on observed data and availability of the descriptive model/simulator. Approximate Bayesian computation (ABC) is an established method for such problems, and involves sampling parameter values from a specified prior distribution. The sampled parameters are then simulated and compared to observed data using a distance function, and often in terms of low-level features (summary statistics). If the simulated output is close enough to observed data within a tolerance bound, the sample is accepted. Once a desired number of accepted samples have been accumulated, they form the posterior distribution of inferred parameters. In practice, ABC parameter inference can be slow and might require a large number of rejection sampling iterations. However, in recent times there has been a lot of progress on improving various aspects of ABC, including selection of priors, summary statistic selection and use of adaptive tolerance bounds.
Selected Research
Learning Summary Statistics With Deep Neural Networks
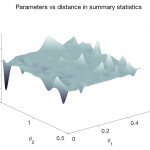
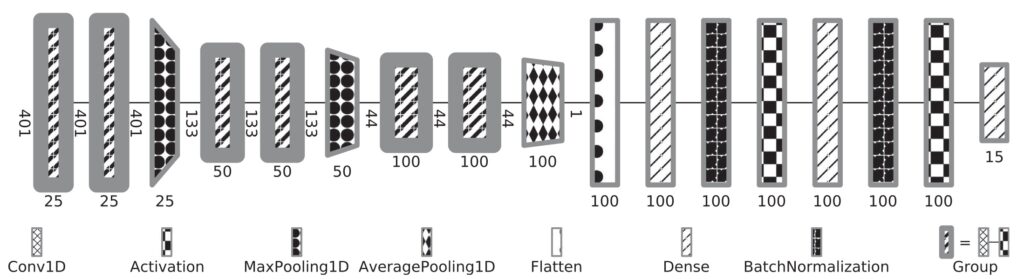
The use of informative summary statistics is crucial for accurate parameter inference. Methods for selecting approximate-sufficient summary statistics exist, but do not scale well with the number of candidate statistics. In recent years, learning high-quality summary statistics using regression models that map simulator output (e.g., time series) to estimated posterior mean, and minimise the squared loss has gained popularity. We propose convolutional architectures owing to their applicability to structured data, for use with simulator models involving time series (structured 1d input). We comprehensively evaluate the convolutional architecture, particularly on parameter inference problems involving complex biochemical reaction networks [1].
We further propose robust and data-efficient Bayesian convolutional networks that offer improvements with respect to overfitting performance, resilience to noise, etc. [2].
[1] Åkesson, M., Singh, P., Wrede, F., & Hellander, A. (2021). Convolutional neural networks as summary statistics for approximate bayesian computation. IEEE/ACM Transactions on Computational Biology and Bioinformatics.
[2] Wrede, F., Eriksson, R., Jiang, R., Petzold, L., Engblom, S., Hellander, A., & Singh, P. (2022, July). Robust and integrative Bayesian neural networks for likelihood-free parameter inference. In 2022 International Joint Conference on Neural Networks (IJCNN) (pp. 1-10). IEEE.

Scalable Inference, Optimization, and Parameter Exploration (Sciope) Toolbox
The Sciope toolbox implements our state-of-the-art summary statistic neural networks, SMC-ABC and Replenishment SMC-ABC parameter inference methods, associated machinery, and basic statistical sampling and optimization methods. The toolbox supports parallelization via Dask and uses the Tensorflow library for deep learning support. Sciope is also used as a backend for parameter inference workflows in StochSS (Stochastic Simulation Service).
[1] Singh, P., Wrede, F., & Hellander, A. (2021). Scalable machine learning-assisted model exploration and inference using Sciope. Bioinformatics, 37(2), 279-281.
[2] Jiang, R., Jacob, B., Geiger, M., Matthew, S., Rumsey, B., Singh, P., … & Petzold, L. (2021). Epidemiological modeling in stochss live!. Bioinformatics, 37(17), 2787-2788.
[3] Drawert, B., Hellander, A., Bales, B., Banerjee, D., Bellesia, G., Daigle Jr, B. J., … & Petzold, L. R. (2016). Stochastic simulation service: bridging the gap between the computational expert and the biologist. PLoS computational biology, 12(12), e1005220.
Surrogate Models of Summary Statistics
Parameter inference problems sometimes consist of highly complex simulators. As an example, stochastic biochemical reaction networks in computational biology often involve tens of reactions taking place among several interacting proteins. The number of control parameters of the simulator may be several tens. Using such a complex simulation model often incurs substantial computational cost in inference.
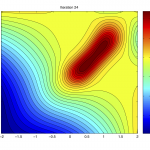
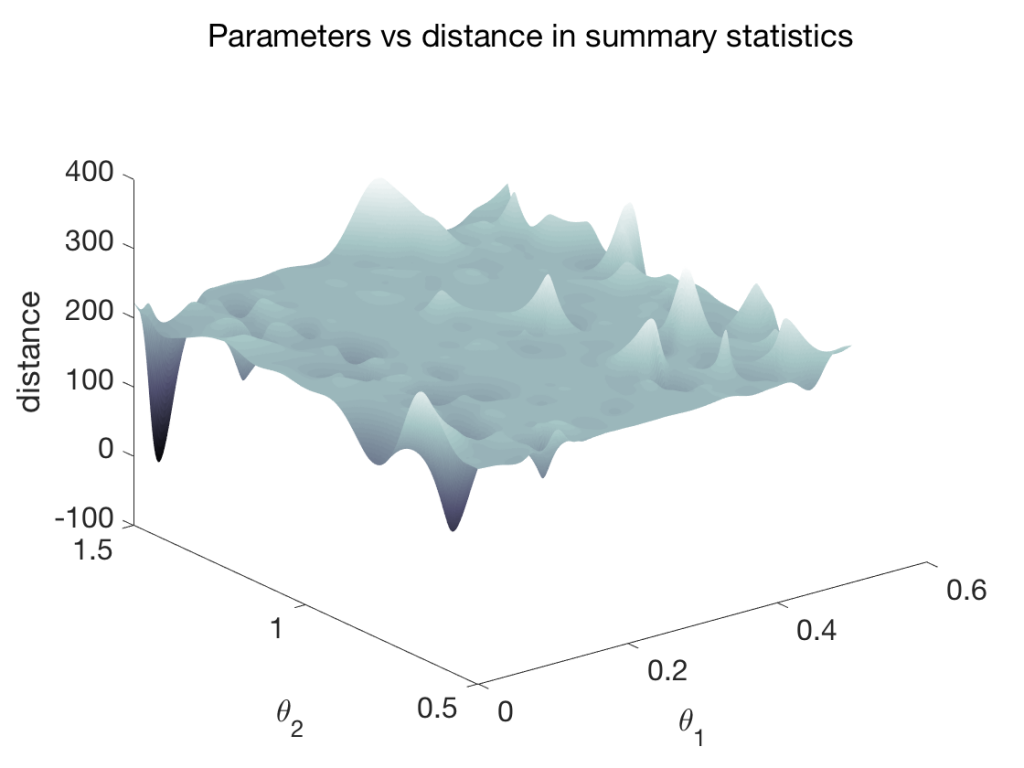
An efficient approach is to train a surrogate model [1] of only the species of interest, taking part in the parameter inference process. The surrogate model learns the mapping from the parameter space (thetas) to the summary statistic space (figure right-top). The prediction times for ~15000 samples for a test problem of 6 parameters is shown in the table (right-bottom). The surrogate model delivers several orders of magnitude speed-up. The surrogate model can be optimized to obtain a point-estimate of inferred parameters, or coupled with a density estimator to conduct parameter inference.
[1] Singh, P., & Hellander, A. (2017, December). Surrogate assisted model reduction for stochastic biochemical reaction networks. In Proceedings of the 2017 Winter Simulation Conference (p. 138). IEEE Press.
Selected Work
Some of our recent work in the area is listed below.


Fronk C; Yun J; Singh P; Petzold. L
Bayesian polynomial neural networks and polynomial neural ordinary differential equations. Journal Article
In: PLOS Computational Biology, 2024.
@article{nokey,
title = {Bayesian polynomial neural networks and polynomial neural ordinary differential equations.},
author = {Colby Fronk and Jaewoong Yun and Prashant Singh and Linda Petzold.},
doi = {arXiv:2308.10892},
year = {2024},
date = {2024-08-01},
urldate = {2023-08-01},
journal = {PLOS Computational Biology},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Enberg R; Costa M F; Koay Y S; Moretti S; Singh P; Waltari H
Enhancing Robustness: BSM Parameter Inference with n1D-CNN and Novel Data Augmentation Conference Forthcoming
European AI for Fundamental Physics Conference (to appear), Forthcoming.
@conference{nokey,
title = {Enhancing Robustness: BSM Parameter Inference with n1D-CNN and Novel Data Augmentation},
author = {Rikard Enberg and Max Fusté Costa and Yong Sheng Koay and Stefano Moretti and Prashant Singh and Harri Waltari},
year = {2024},
date = {2024-04-30},
booktitle = {European AI for Fundamental Physics Conference (to appear)},
keywords = {},
pubstate = {forthcoming},
tppubtype = {conference}
}
Cheng L; Singh P; Ferranti F
Transfer learning-assisted inverse modeling in nanophotonics based on mixture density networks Journal Article
In: IEEE Access, vol. 12, pp. 55218-55224, 2024.
@article{cheng2024transfer,
title = {Transfer learning-assisted inverse modeling in nanophotonics based on mixture density networks},
author = {Liang Cheng and Prashant Singh and Francesco Ferranti},
url = {https://ieeexplore.ieee.org/abstract/document/10486893},
doi = {10.1109/ACCESS.2024.3383790},
year = {2024},
date = {2024-04-02},
urldate = {2024-01-01},
journal = {IEEE Access},
volume = {12},
pages = {55218-55224},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Enberg R; Costa M F; Koay Y S; Moretti S; Singh P; Waltari H
BSM models and parameter inference via an n-channel 1D-CNN Conference
Sixth annual workshop of the LPCC inter-experimental machine learning working group, CERN, Geneva, 2024.
@conference{nokey,
title = {BSM models and parameter inference via an n-channel 1D-CNN},
author = {Rikard Enberg and Max Fusté Costa and Yong Sheng Koay and Stefano Moretti and Prashant Singh and Harri Waltari},
url = {https://indico.cern.ch/event/1297159/contributions/5729212/attachments/2789892/4865115/IML3.pdf},
year = {2024},
date = {2024-01-12},
urldate = {2024-01-12},
booktitle = {Sixth annual workshop of the LPCC inter-experimental machine learning working group, CERN, Geneva},
keywords = {},
pubstate = {published},
tppubtype = {conference}
}
Coulier A; Singh P; Sturrock M; Hellander A
Systematic comparison of modeling fidelity levels and parameter inference settings applied to negative feedback gene regulation Journal Article
In: PLOS Computational Biology, vol. 18, no. 12, pp. e1010683, 2022.
@article{coulier2022systematic,
title = {Systematic comparison of modeling fidelity levels and parameter inference settings applied to negative feedback gene regulation},
author = {Adrien Coulier and Prashant Singh and Marc Sturrock and Andreas Hellander},
url = {https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1010683},
doi = {https://doi.org/10.1371/journal.pcbi.1010683},
year = {2022},
date = {2022-01-01},
urldate = {2022-01-01},
journal = {PLOS Computational Biology},
volume = {18},
number = {12},
pages = {e1010683},
publisher = {Public Library of Science San Francisco, CA USA},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Wrede F; Eriksson R; Jiang R; Petzold L; Engblom S; Hellander A; Singh P
Robust and integrative Bayesian neural networks for likelihood-free parameter inference Proceedings Article
In: 2022 International Joint Conference on Neural Networks (IJCNN), pp. 1–10, IEEE 2022.
@inproceedings{wrede2022robust,
title = {Robust and integrative Bayesian neural networks for likelihood-free parameter inference},
author = {Fredrik Wrede and Robin Eriksson and Richard Jiang and Linda Petzold and Stefan Engblom and Andreas Hellander and Prashant Singh},
url = {https://ieeexplore.ieee.org/abstract/document/9892800
https://arxiv.org/pdf/2102.06521},
doi = {https://doi.org/10.1109/IJCNN55064.2022.9892800},
year = {2022},
date = {2022-01-01},
urldate = {2022-01-01},
booktitle = {2022 International Joint Conference on Neural Networks (IJCNN)},
pages = {1--10},
organization = {IEEE},
keywords = {},
pubstate = {published},
tppubtype = {inproceedings}
}
Jiang R; Jacob B; Geiger M; Matthew S; Rumsey B; Singh P; Wrede F; Yi T; Drawert B; Hellander A; others
Epidemiological modeling in stochss live! Journal Article
In: Bioinformatics, vol. 37, no. 17, pp. 2787–2788, 2021.
@article{jiang2021epidemiological,
title = {Epidemiological modeling in stochss live!},
author = {Richard Jiang and Bruno Jacob and Matthew Geiger and Sean Matthew and Bryan Rumsey and Prashant Singh and Fredrik Wrede and Tau-Mu Yi and Brian Drawert and Andreas Hellander and others},
url = {https://academic.oup.com/bioinformatics/article/37/17/2787/6123781
https://academic.oup.com/bioinformatics/advance-article-pdf/doi/10.1093/bioinformatics/btab061/40342592/btab061.pdf},
doi = {https://doi.org/10.1093/bioinformatics/btab061},
year = {2021},
date = {2021-01-01},
urldate = {2021-01-01},
journal = {Bioinformatics},
volume = {37},
number = {17},
pages = {2787--2788},
publisher = {Oxford University Press},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Akesson M; Singh P; Wrede F; Hellander A
Convolutional neural networks as summary statistics for approximate bayesian computation Journal Article
In: IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2021.
@article{akesson2021convolutional,
title = {Convolutional neural networks as summary statistics for approximate bayesian computation},
author = {Mattias Akesson and Prashant Singh and Fredrik Wrede and Andreas Hellander},
url = {https://ieeexplore.ieee.org/abstract/document/9525290},
doi = {https://doi.org/10.1109/TCBB.2021.3108695},
year = {2021},
date = {2021-01-01},
urldate = {2021-01-01},
journal = {IEEE/ACM Transactions on Computational Biology and Bioinformatics},
publisher = {IEEE},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Jiang R M; Wrede F; Singh P; Hellander A; Petzold L R
Accelerated regression-based summary statistics for discrete stochastic systems via approximate simulators Journal Article
In: BMC bioinformatics, vol. 22, no. 1, pp. 1–17, 2021.
@article{jiang2021accelerated,
title = {Accelerated regression-based summary statistics for discrete stochastic systems via approximate simulators},
author = {Richard M Jiang and Fredrik Wrede and Prashant Singh and Andreas Hellander and Linda R Petzold},
url = {https://link.springer.com/article/10.1186/s12859-021-04255-9},
doi = {https://doi.org/10.1186/s12859-021-04255-9},
year = {2021},
date = {2021-01-01},
urldate = {2021-01-01},
journal = {BMC bioinformatics},
volume = {22},
number = {1},
pages = {1--17},
publisher = {BioMed Central},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Singh P; Hellander A
Surrogate assisted model reduction for stochastic biochemical reaction networks Proceedings Article
In: 2017 Winter Simulation Conference (WSC), pp. 1773–1783, IEEE 2017.
@inproceedings{singh2017surrogate,
title = {Surrogate assisted model reduction for stochastic biochemical reaction networks},
author = {Prashant Singh and Andreas Hellander},
url = {https://ieeexplore.ieee.org/abstract/document/8247915
},
doi = {https://doi.org/10.1109/WSC.2017.8247915},
year = {2017},
date = {2017-01-01},
urldate = {2017-01-01},
booktitle = {2017 Winter Simulation Conference (WSC)},
pages = {1773--1783},
organization = {IEEE},
keywords = {},
pubstate = {published},
tppubtype = {inproceedings}
}