Optimization
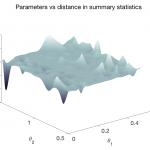
The field of optimization is rich and important, finding wide application across domains. Our research interests have primarily revolved around the theme of data-efficient optimization. Scientific computing and eScience have popularized simulation-driven design and analysis of (sub)systems. Simulations in certain applications like CFD, electrical engineering, structural engineering, etc. can often be computationally expensive. Therefore, optimization problems involving such simulators necessitate data-efficient methods in order to deliver solutions in practical and product-critical timeframes.
Optimization can also be viewed as a sampling problem. Optimization algorithms select samples at well-chosen locations to make sense of the objective function landscape. The search for optima then proceeds in the direction offering greater promise based on current knowledge. Therefore, there is always a sense of uncertainty owing to gaps in knowledge, i.e., non-sampled space.
Probabilistic models provide a powerful framework of dealing with this uncertainty. Bayesian optimization embodies this spirit, and involves a Gaussian process (GP) model learning the objective function landscape coupled with a sequential sampling algorithm making use of uncertainty estimates of the GP model to drive the search towards the optima.
Selected Research
Bayesian Optimization
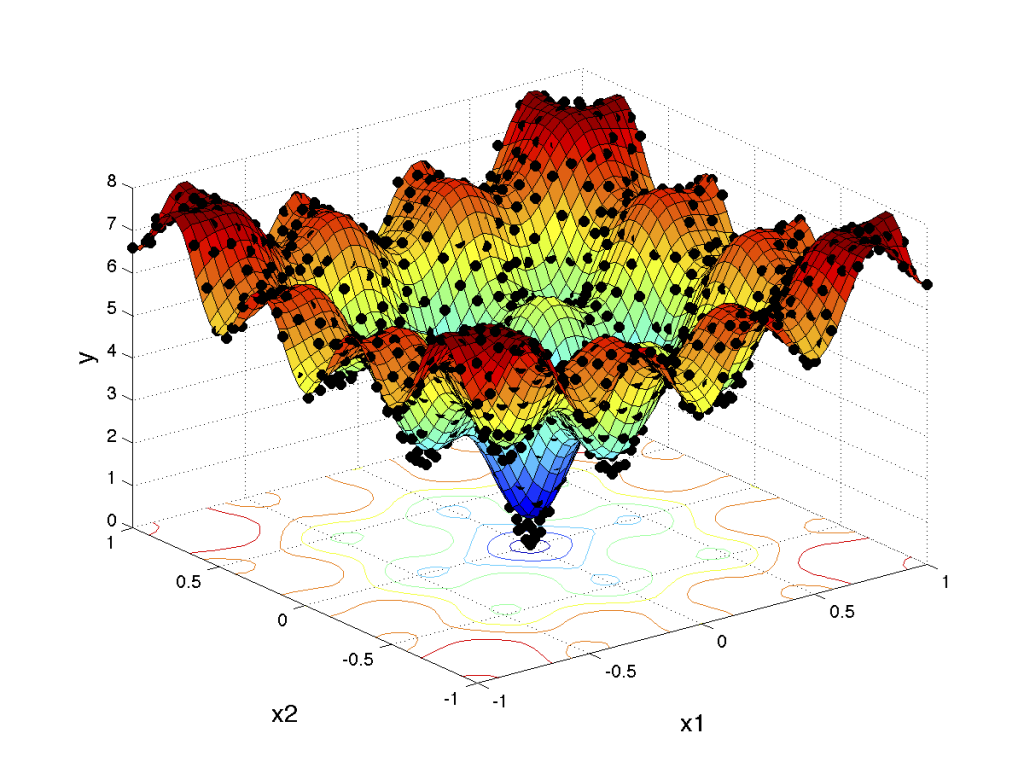
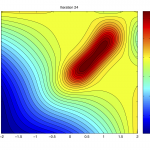
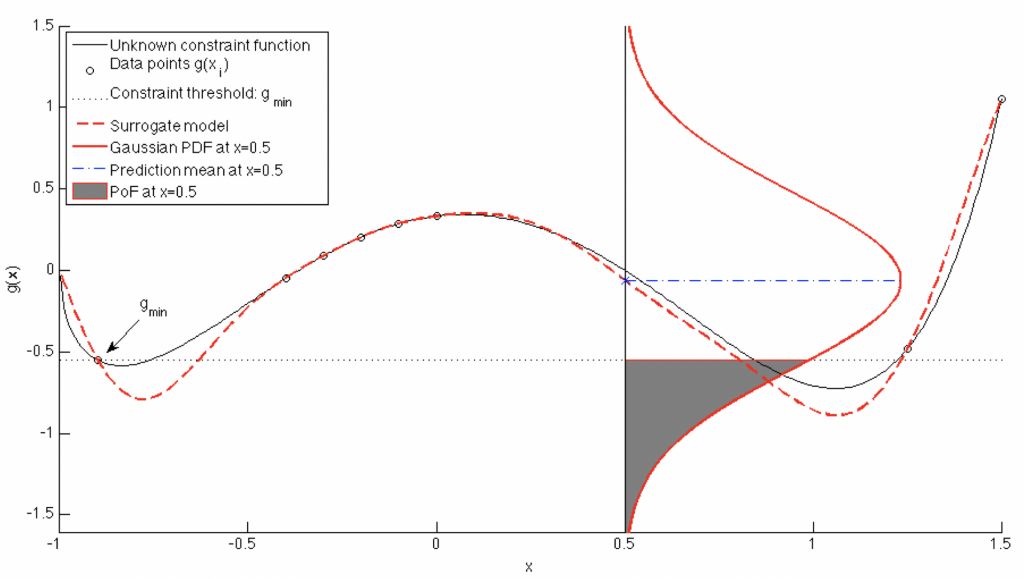
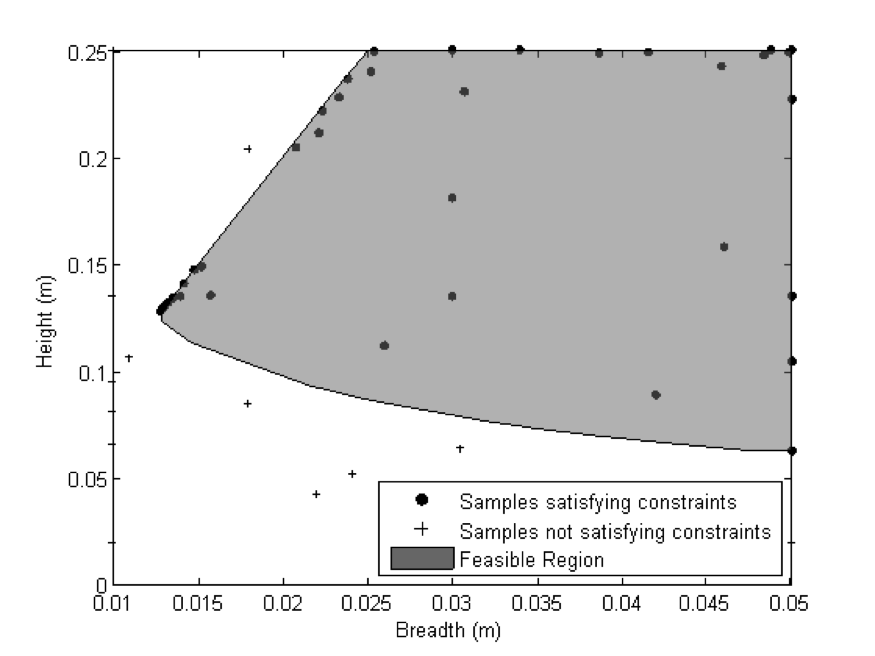
A trained Gaussian process (GP) (or Kriging) surrogate model can be used to evaluate a large number of Monte-Carlo candidate samples throughout the input range. For any given candidate, it is possible to obtain the PDF using the GP surrogate. As shown in the accompanying figure on the right, the probability of improvement (PoI) over the current minima (g_min) can easily be computed as the shaded region. The related metric of probability of feasibility (PoF) [1] is analogous to PoI but applies to constraint functions instead of objective functions. The expected improvement (EI) criterion is similar in nature, but rather than computing the probability of improving over the current minima, computes the value of expected improvement over the current minima.
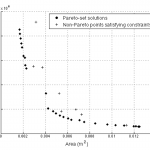
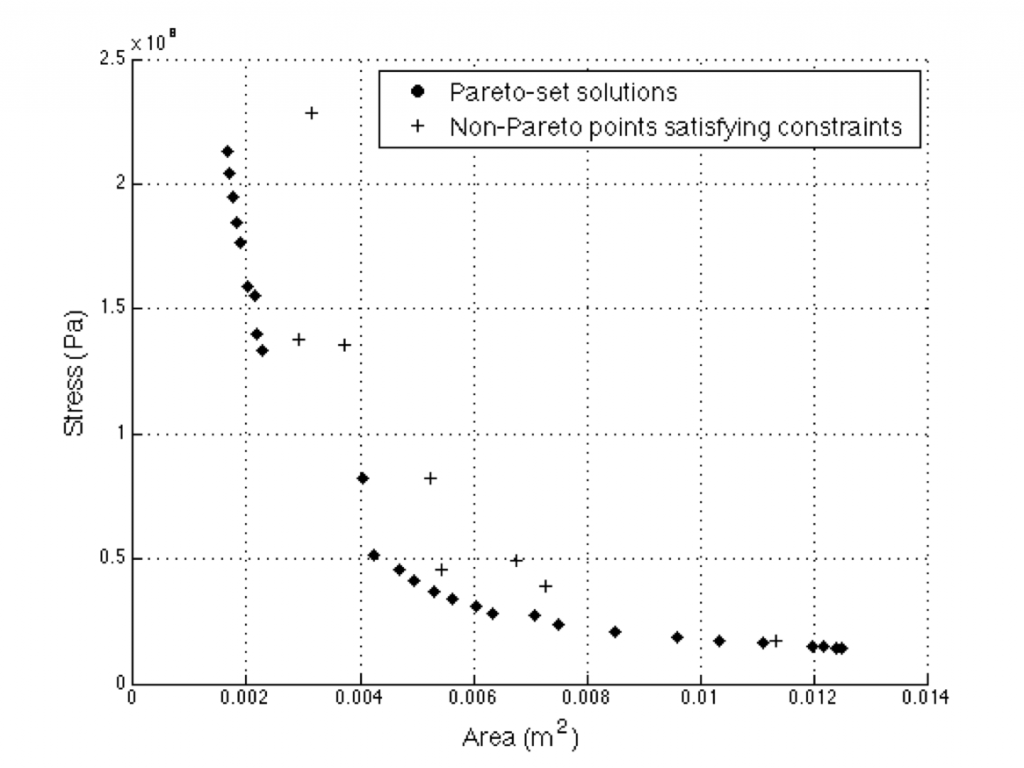
Sampling using these metrics therefore corresponds to exploitation in the exploration versus exploitation spectrum. The figure on the right shows a dense cluster of points selected using PoF in the edge of the feasible region. The true optima also lies in the same region. The PoF metric was able to quickly zoom-in towards promising areas. Both single and multi-objective formulations of the metrics are possible [1-3]. Formally, Bayesian optimization involves GP or Kriging models but in principle, any probabilistic model (such as probabilistic SVM) can be employed.
[1] Singh, P., Couckuyt, I., Ferranti, F., & Dhaene, T. (2014, July). A constrained multi-objective surrogate-based optimization algorithm. In 2014 IEEE Congress on Evolutionary Computation (CEC) (pp. 3080-3087). IEEE.
[2] Singh, P., Couckuyt, I., Elsayed, K., Deschrijver, D., & Dhaene, T. (2016). Shape optimization of a cyclone separator using multi-objective surrogate-based optimization. Applied Mathematical Modelling, 40(5-6), 4248-4259.
[3] Singh, P., Rossi, M., Couckuyt, I., Deschrijver, D., Rogier, H., & Dhaene, T. (2017). Constrained multi‐objective antenna design optimization using surrogates. International Journal of Numerical Modelling: Electronic Networks, Devices and Fields, 30(6), e2248.
Surrogate-Based Optimization
In cases where the objective function is computationally expensive to evaluate, a fast approximation in the form of a surrogate model or metamodel can be trained using a global surrogate modeling algorithm [1,2]. The surrogate can then be used in lieu of the objective function with a traditional optimization algorithm or even heuristic-based methods. Interestingly, one of the drawbacks of evolutionary optimization algorithms is that they typically require a large number of objective function evaluations to converge. This makes them unsuitable for computationally expensive objective functions. The use of surrogates however allows evaluation within fractions of a second, and makes the problem amenable for evolutionary optimization [3].
[1] Singh, P., Deschrijver, D., & Dhaene, T. (2013, December). A balanced sequential design strategy for global surrogate modeling. In 2013 Winter Simulations Conference (WSC) (pp. 2172-2179). IEEE.
[2] Singh, P., Van Der Herten, J., Deschrijver, D., Couckuyt, I., & Dhaene, T. (2017). A sequential sampling strategy for adaptive classification of computationally expensive data. Structural and Multidisciplinary Optimization, 55(4), 1425-1438.
[3] Singh, P., Couckuyt, I., Elsayed, K., Deschrijver, D., & Dhaene, T. (2017). Multi-objective geometry optimization of a gas cyclone using triple-fidelity co-kriging surrogate models. Journal of Optimization Theory and Applications, 175(1), 172-193.